Publications▾ Expand All Digests ▾
S. Xue et al.
Mapping and Analyzing the Topographic Roughness of the Moon Using A Coarse-Graining Decomposition.
Journal of Geophysical Research: Planets (accepted) ▾ Digest ▾

Short description goes here.
S. Kouhen et al.
Convective and orographic origins of the mesoscale kinetic energy spectrum.
(Submitted) ▾ Digest ▾

Short description goes here.
A. Leong et al.
A combined speckle- & propagation-based single shot two-dimensional phase retrieval method.
(Submitted) ▾ Digest ▾

Short description goes here.
H. Khatri et al.
A scale-dependent analysis of the barotropic vorticity budget in a global ocean simulation.
Journal of Advances in Modeling Earth Systems, 16(6), e2023MS003813 (2024) ▾ Digest ▾

Short description goes here.
K. Kurzer-Ogul et al.
Radiation and heat transport in divergent shock-bubble interactions.
Physics of Plasmas, 31, 032304 (2024) ▾ Digest ▾
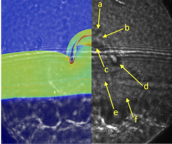
Shock-bubble interactions (SBI) are important across a wide range of physical systems. In inertial confinement fusion (ICF), interactions between laser-driven shocks and micro-voids in both ablators and foam targets generate instabilities that are a major obstacle in achieving ignition. Experiments imaging the collapse of such voids at high energy densities (HED) are constrained by spatial and temporal resolution, making simulations a vital tool in understanding these systems. This work, led by Kelin, investigates the role of various physical processes (radiation transport, heat conduction, hydrodynamic instabilities) and compares the output to data from experiments carried out at the Linear Coherent Light Source (LCLS).
B. Storer et al.
Global cascade of kinetic energy in the ocean and the atmospheric imprint.
Science Advances, 9, eadi7420 (2023) ▾ Digest ▾
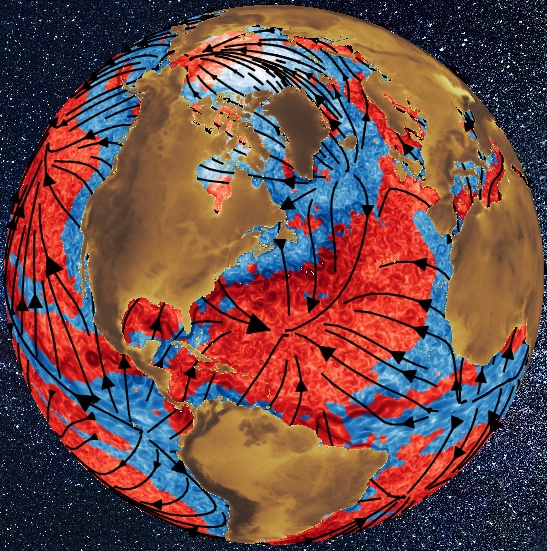
This work, led by Ben, carried out the first global ocean-energy scale-analysis made possible by a new coarse-graining framework we developed on the sphere. It has been suggested by recent studies that mesoscale ocean eddies O(100) km in size may play a substantial role in climate variability. Such oceanic internal variability was hypothesized to arise because energy can be transferred between seemingly incoherent mesoscale eddies and the larger scale coherent flow, which evolves on the long timescales of climate and is directly coupled to it. In this work, we provide direct evidence of such transfer, although the mechanism responsible for the transfer is different from what had been hypothesized. The mechanism involves the atmospheric circulation. We show how the ocean weather systems self-organize via an upscale cascade. We also identify (for the first time) a two-way coupling between these seemingly incoherent ocean eddies and the climate-scale circulation of the ocean and atmosphere. Previous studies of oceanic scale-transfer relied on performing Fourier analysis in boxes, which had prevented access to planetary scales that couple directly to climate. By quantifying the global transfer of energy across-scales, we believe this work demonstrates a potent framework for tackling the problem of multiscale coupling within the climate system.
D. Zhao and H. Aluie
Measuring scale-dependent shape anisotropy by coarse-graining: Application to inhomogeneous Rayleigh-Taylor turbulence
Physical Review Fluids, 8, 114601 (2023) ▾ Digest ▾
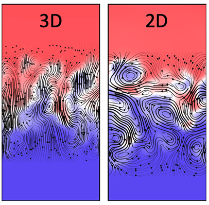
This work, led by Dongxiao, generalizes the "filtering spectrum" [Sadek & Aluie 2018] to probe scales along different directions by spatial coarse-graining. This multi-dimensional filtering spectrum quantifies the spectral content of flows that are not necessarily homogeneous. From multi-dimensional spectral information, we propose a simple metric for shape anisotropy at various scales. The method is applied to simulations of 2D and 3D Rayleigh-Taylor (RT) turbulence, which is inhomogeneous and anisotropic. We show that 3D RT has clear shape anisotropy at large scales with approximately $4:3$ vertical to horizontal aspect ratio, but tends toward isotropy at small scales as expected. In sharp contrast, we find that RT in 2D simulations, which are still the main modeling framework for many applications, is isotropic at large scales and its shape anisotropy increases at smaller scales where structures tend to be horizontally elongated. While this may be surprising, it is consistent with recent results that large-scale isotropy in 2D RT is due to the generation of a large-scale overturning circulation via an upscale cascade, while small scale anisotropy is due to the stable stratification resultant from such overturning and the inefficient mixing in 2D.
D. Soltani and H. Aluie
On Galilean Invariance of Mean Kinetic Helicity.
Physics of Fluids, 35, 121701 (2023) ▾ Digest ▾
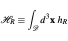
While kinetic helicity is not Galilean invariant locally, it is known [Moffatt, 1969] that its spatial integral quantifies the degree of knottedness of vorticity field lines. Being a topological property of the flow, mean kinetic helicity is Galilean invariant. Here, we provide a direct mathematical proof that kinetic helicity is Galilean invariant when spatially integrated over regions enclosed by vorticity surfaces, i.e., surfaces of zero vorticity flux. We also discuss so-called "relative" kinetic helicity, which is Galilean invariant when integrated over any region in the flow.
H. Yin et al.
Energy transfer and scale dynamics in 2D and 3D laser driven jets.
Physics of Plasmas, 30, 092309 (2023) ▾ Digest ▾
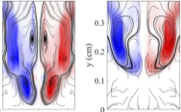
This work, led by Hao, demonstrates a methodology for diagnosing the multiscale dynamics and energy transfer in complex HED flows with realistic driving and boundary conditions. The approach separates incompressible, compressible, and baropycnal contributions to energy scale-transfer and quantifies the direction of these transfers in (generalized) wavenumber space. We use this to compare the kinetic energy (KE) transfer across scales in simulations of 2D axisymmetric versus fully 3D laser driven plasma jets. Due to exorbitant computing costs of 3D simulations, 2D simulations will remain for the foreseeable future the main modeling framework for many applications in fusion and high energy density science. We show that, in addition to its well known bias for underestimating hydrodynamic instability growth, 2D modeling suffers from significant spurious energization of the bulk flow by a turbulent upscale cascade. The methodology presented here may help with inter-model comparison and validation, including future modeling efforts to alleviate some of the 2D hydrodynamic artefacts highlighted in this study.
S. Rai et al.
Scale-dependent air-sea mechanical coupling: Resolution mismatch and spurious eddy killing.
(Submitted) ▾ Digest ▾

Short description goes here.
D. Zhao et al.
Lagrangian investigation of the interface dynamics in single-mode Rayleigh-Taylor instability.
Physics of Fluids, 35, 104103 (2023) ▾ Digest ▾

Short description goes here.
M. Buzzicotti et al.
Spatio-temporal coarse-graining decomposition of the global ocean geostrophic kinetic energy.
Journal of Advances in Modeling Earth Systems, 15(6), e2023MS003693 (2023) ▾ Digest ▾
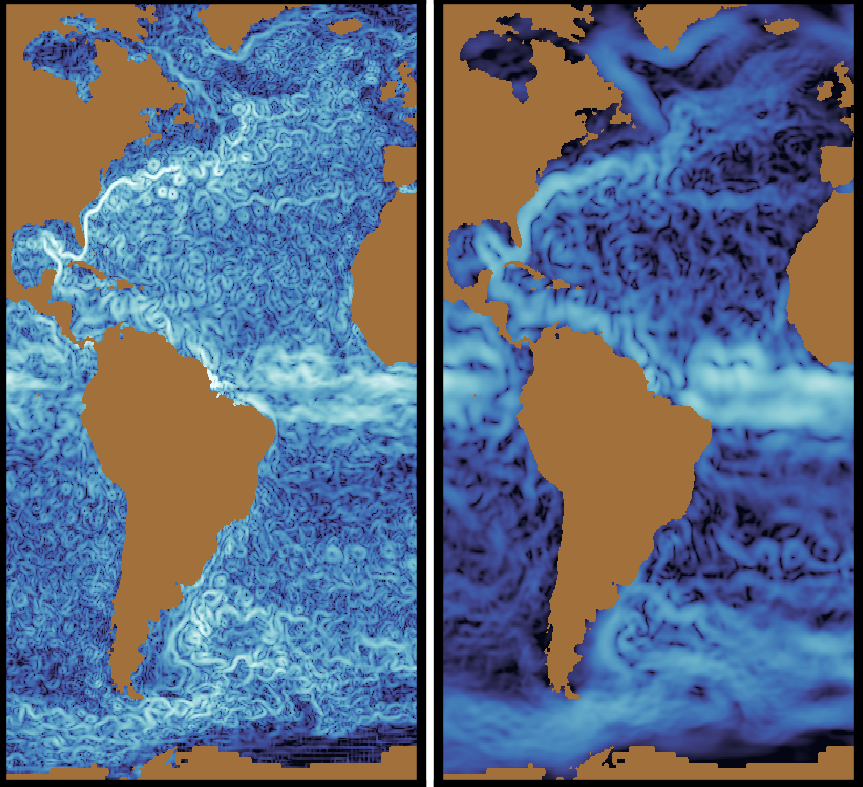
This work, led by Michele and Ben, expands on a recent determination of the first global energy spectrum of the ocean's surface geostrophic circulation (Storer+2022) using a coarse-graining (CG) method. We compare spectra from CG to those from spherical harmonics by treating land in a manner consistent with the boundary conditions. While the two methods yield qualitatively consistent domain-averaged results, spherical harmonics spectra are too noisy at gyre-scales (>1000 km). More importantly, spherical harmonics are inherently global and cannot provide local information connecting scales with currents geographically. CG shows that the extra-tropics mesoscales (100--500 km) have a root-mean-square (rms) velocity of ~15 cm/s, which increases to ~30--40 cm/s locally in the Gulf Stream and Kuroshio and to ~16--28 cm/s in the ACC. There is notable hemispheric asymmetry in mesoscale energy-per-area, which is higher in the north due to continental boundaries. We estimate that ~25--50 % of total geostrophic energy is at scales smaller than 100 km, and is un(der)-resolved by pre-SWOT satellite products. Spectra of the time-mean component show that most if its energy (up to 70\%) resides in stationary mesoscales (<500 km), highlighting the preponderance of 'standing' small-scale structures in the global ocean. By coarse-graining in space and time, we compute the first spatio-temporal global spectrum of geostrophic circulation from AVISO and NEMO. These spectra show that every length-scale evolves over a wide range of time-scales with a consistent peak at ~200 km and ~2--3 weeks.
B. Storer and H. Aluie
Flowsieve: A coarse-graining utility for geophysical flows on the sphere.
Journal of Open Source Software, 8(84), 4277 (2023) ▾ Digest ▾

Short description goes here.
H. Aluie et al.
Effective drift velocity from turbulent transport by vorticity.
Physical Review Fluids 7, 104601 (2022) ▾ Digest ▾
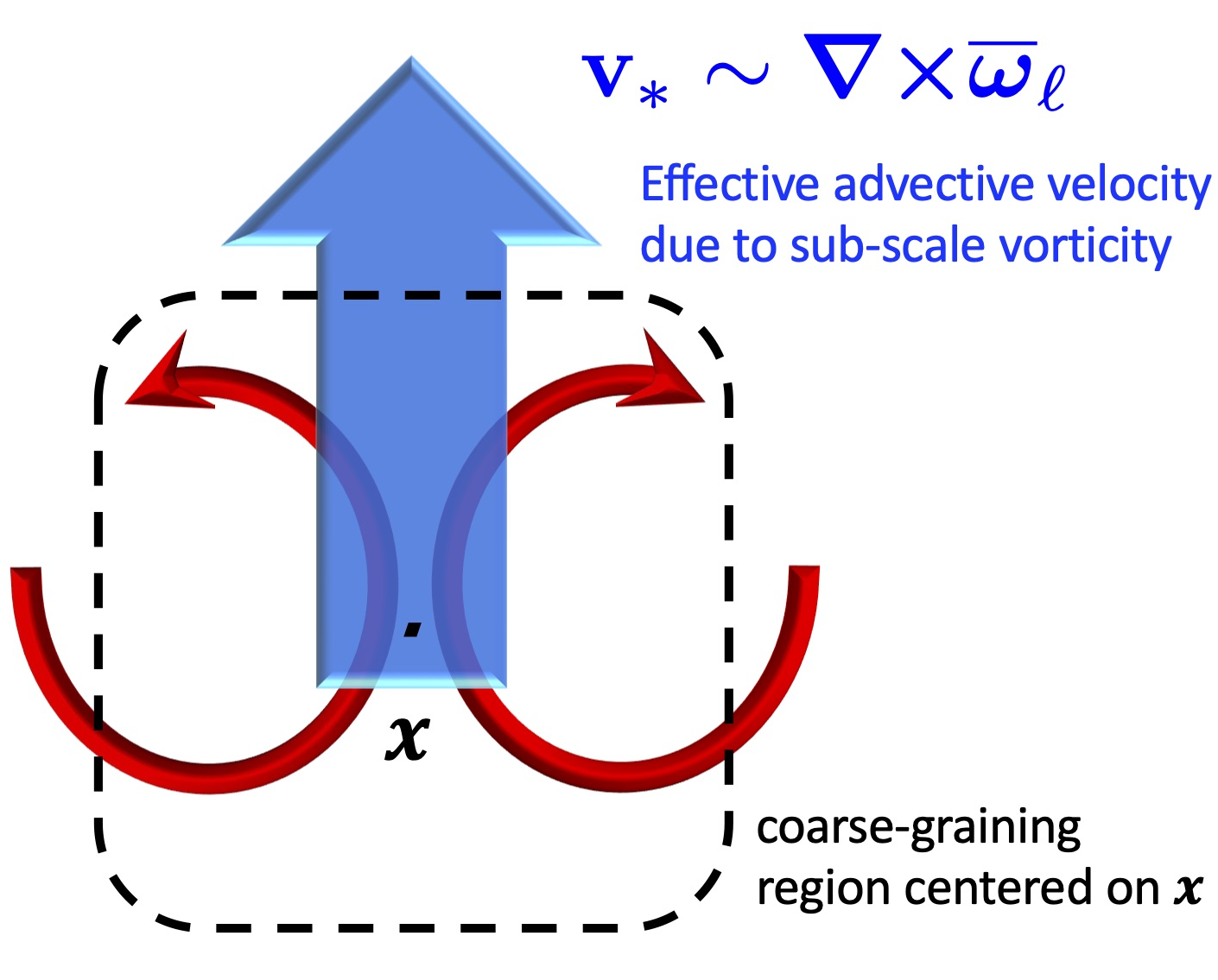
Short description goes here.
D. Hodge et al.
Multi-frame, ultrafast, x-ray microscope for imaging shockwave dynamics.
Optics Express, 30, 38405-38422 (2022) ▾ Digest ▾
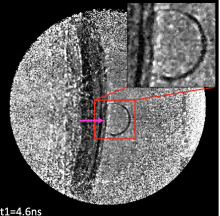
Laboratory experiments in high energy density science are crucial to mimic conditions that exists in the interior of stars and planets and also in realizing inertial confinement fusion (ICF) as a viable energy source for humanity. However, such experiments on laser-driven targets are impeded by our lack of sufficient knowledge and control of defects such as micro-voids in the target material. It is critical to understand how these micro-voids interact with the laser-driven shock waves that compress the target. At the Matter in Extreme Conditions (MEC) instrument at the Linac Coherent Light Source (LCLS), we utilized an x-ray pulse train with nanosecond separation, an x-ray microscope, and an ultrafast x-ray imaging (UXI) detector to image shock wave interactions with micro-voids.
S. Pandolfi et al.
Novel Fabrication Tools for Dynamic Compression Targets with Engineered Voids Using Photolithography Methods
Review of Scientific Instruments 93, 103502 (2022) ▾ Digest ▾
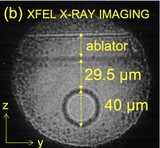
Mesoscale imperfections, such as pores and voids, can strongly modify the properties and the mechanical response of materials under extreme conditions. Tracking the material response and microstructure evolution during void collapse is crucial for understanding its performance. In particular, imperfections in the ablator materials, such as voids, can limit the efficiency of the fusion reaction and ultimately hinder ignition. To characterize how voids influence the response of materials during dynamic loading and seed hydrodynamic instabilities, we have developed a tailored fabrication procedure for designer targets with voids at specific locations. Insight from shock compression experiments will provide benchmarks for the next generation of microphysics modeling.
M. Buzzicotti et al.
A Coarse-grained Decomposition of Surface Geostrophic Kinetic Energy in the Global Ocean.
(Submitted) ▾ Digest ▾
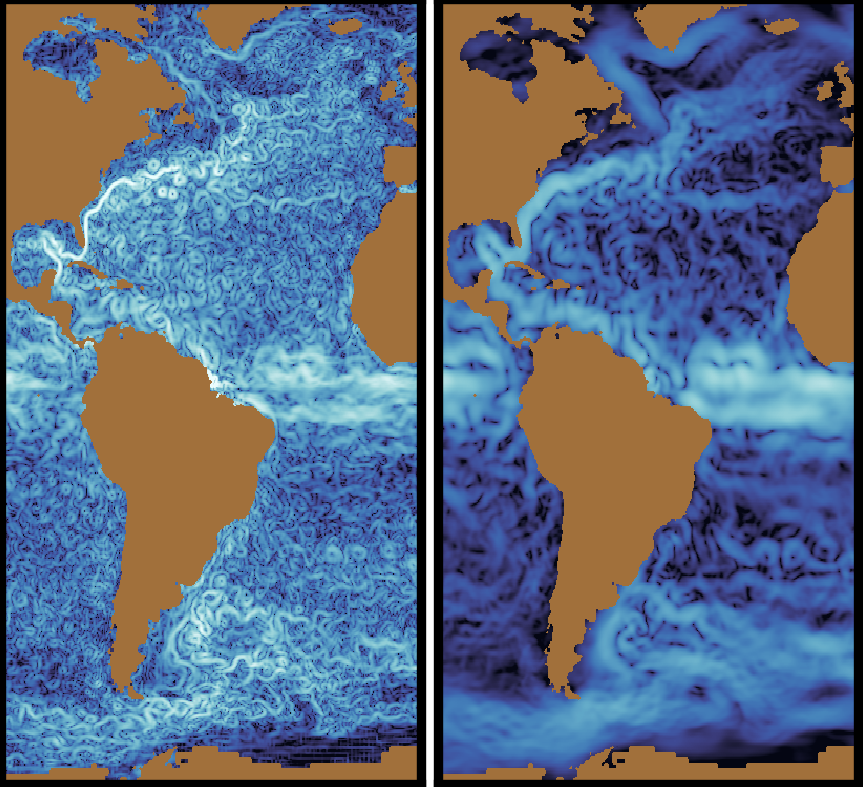
Short description goes here.
F. Garcia-Rubio et al.
Theory of the Magnetothermal Instability in Coronal Plasma Flows
Physics of Plasmas 29, 092106 (2022) ▾ Digest ▾
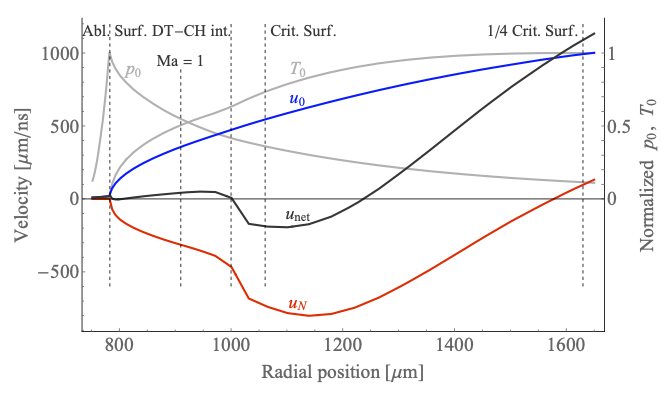
This work, led by Fernando, develops a complete theory for the evolution of the magnetothermal instability (MTI) in radiation-driven plasmas. It has long been known that self-generated magnetic (B) fields develop in radiation-driven plasmas, such as in astrophysical systems illuminated by stars or in terrestrial laboratories in laser-driven plasmas such as in inertial confinement fusion (ICF) applications. These B fields can play an important role in the evolution of the system because they modify heat transfer and seed hydrodynamic instabilities. The instabilities often discussed in radiation-driven plasmas are of a hydrodynamic nature and have time scales given by the plasma conditions at the ablation front. However, the self-generated B fields can trigger another instability on its own in the light, hot plasma of the corona. This instability, known as magnetothermal instability (MTI), was first described in the seminal paper by Tidman and Shanny. However the Tidman and Shanny work ignored the hydrodynamics. This work carries out a more complete analysis by incorporating the effects of the flow and shows that the MTI can be an absolute instability under certain flow conditions.
B. Storer et al.
Global energy spectrum of the general oceanic circulation.
Nature Communications, 13, 5314 (2022) ▾ Digest ▾

This work, led by Ben, measured for the first time the truly global wavenumber spectrum of the general oceanic circulation. To do so, we used (i) a method for calculating spectra using coarse-graining (paper1) + (ii) a method for spatial coarse-graining on the sphere (paper2) + (iii) Flowsieve: an efficient parallel code, which we've made publicly available. Our measurement allows us to make several exciting findings: (1) The spectral peak is at ~9,000km and due to the Antarctic Circumpolar Current. It is not at the mesoscales O(100)km as is often claimed. (2) There is E(k)~k^{-1} power-law scaling at "gyre-scales" >1000km not observed before. (3) Existence of scale separation between the gyre-scales >1000km and mesoscales <500km, with the latter showing a peak at ~300km. (4) A clear drift in the seasonal cycle of larger scales, ~40 days/octave of scales, such that 100km peak in spring, 1000km peak in late summer. (5) Unlike Fourier spectra within small box regions often used in oceanography, this global spectrum integrates to the total energy resolved by the data over the entire globe.
N. Acharya et al.
Numerical investigation of laser-driven shock interaction with a deformable particle.
Physics of Plasmas, 29, 052302 (2022) ▾ Digest ▾
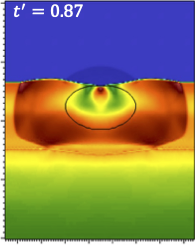
This paper, led by Nitish, investigates numerically the evolution of a metal sphere ~50 microns in diameter embedded in a plastic target and subjected to a laser-driven shock. A simple modification to the ideal gas EOS was developed and employed to describe the target materials and examine the particle dynamics. The modified EOS model presented in this study can be used to approximate solid materials in hydrodynamic codes that lack material strength models.
D. Zhao et al.
Scale Interactions and Anisotropy in Rayleigh-Taylor Turbulence.
Journal of Fluid Mechanics, 930, A29 (2022) ▾ Digest ▾

Building on important work by Cook, Zhou, and Cabot (LLNL), we perform the first analysis of energy transfer across scales in all directions (both homogeneous and inhomogeneous) in Rayleigh-Taylor flows with significant density variation. This allows us to close the energy budget. We identify a spurious feedback loop in 2D that is absent in 3D. In ICF, 2D modeling is still the main 'workhorse' to this day due to its lower computational cost. Our findings indicate that the spurious feedback loop in 2D leads to an artificially enhanced interpenetration of heavy and light fluids (but not enhanced mixing). This leads to incorrect predictions of PdV work on the "hot spot" in implosions from 2D models. Another important conclusion is evidence refuting the notion of "bubble mergers." Despite its wide appeal in the literature, the notion is speculative with little support from evidence. Our measurement of energy transfer between scales indicates that large bubbles do not grow due to the mergers of smaller bubbles, but due to what we call baropycnal work --a conduit for potential energy. The idea that large-scale turbulence is forced by small-scale instabilities is common but may be misleading. Large-scale turbulence is forced by a free energy reservoir present in the system, even if the initial mode perturbation is seeded by the beating of higher modes (smaller scales). Seeding a mode and persistent forcing of a mode are distinct.
S. Rai et al.
Scale of Oceanic Eddy-Killing by Wind from Global Satellite Observations.
Science Advances, 7(28), eabf4920 (2021) ▾ Digest ▾

This work uses a new approach to analyze global oceanic data from both satellites and models. We show that while wind is the primary driver of the oceanic general circulation, it kills the ocean’s most energetic motions --its mesoscale eddies. The length scales at which such air-sea energy transfer occurs over the entire globe had not been studied before, to our knowledge. In fact, we show that the temporal mean-eddy decomposition (i.e. Reynolds averaging) commonly used in oceanography fails to unravel eddy-killing. Our results present the first evidence that eddy killing is a major seasonal sink for the oceanic eddies, peaking in winter. We show that eddy killing removes a substantial fraction (up to 90%) of the wind power input in western boundary currents such as the Gulf Stream and Kuroshio. This process, often overlooked in analyses and models, is a major dissipation pathway for mesoscales, the ocean’s most energetic scales.
X. Bian et al.
Scaling of Turbulent Viscosity and Resistivity: Extracting a Scale-dependent Turbulent Magnetic Prandtl Number.
Astrophysical Journal Letters, 917, L3 (2021) ▾ Digest ▾

Turbulent viscosity and resistivity are perhaps the simplest models for turbulent transport of angular momentum and magnetic fields, respectively. Their ratio is the turbulent magnetic Prandtl number and has been well recognized to determine the final magnetic configuration of accretion disks. In this paper, we developed a new approach to determining these "effective transport" coefficients acting at different length-scales. To our knowledge, our work is the first to calculate the turbulent magnetic Prandtl number as a function of length scale. Our results indicate that it has values of ~1 to 2 at the smallest ideal hydrodynamic scales, increasing to ~5 to 10 at the largest scales. For accretion disks, this indicates that the flow may be more efficient at accreting large-scale magnetic fields radially inward than diffusing them outward, way from the center. In addition to potential implications for astrophysical systems, our analysis of how these effective transport coefficients vary with length-scale provides a practical model for these quantities that does not rely on any particular phenomenology.
F. Garcia-Rubio et al.
Magnetic-Field Generation and its Effect on Ablative Rayleigh-Taylor Instability in Diffusive Ablation Fronts.
Physics of Plasmas, 28, 012103 (2021) [Featured Article] ▾ Digest ▾
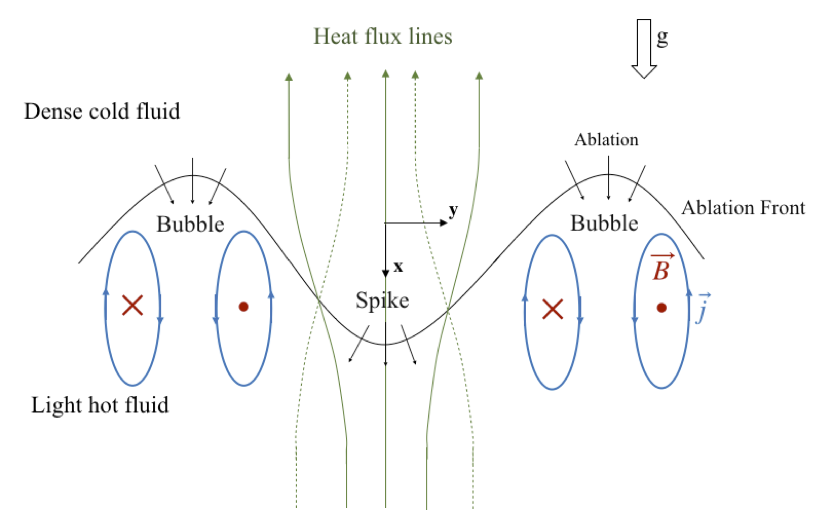
This paper investigates the effects of self-generated magnetic fields on the ablative Rayleigh–Taylor (RT) instability in the linear regime. During the development of the RT instability, magnetic fields are generated due to misalignment between pressure and density gradients via a process called the Biermann-battery. Magnetic fields accumulate at the section of the ablation front where the Nernst and the plasma velocities cancel each other. Magnetic fields modify the dynamics of the instability through the Righi–Leduc term, which acts as a heat source in the energy equation. We find that the magnetic fields affect perturbations with short wavelengths up to the most unstable wave in the spectrum. The magnetic field plays a destabilizing role for moderate Froude numbers and becomes stabilizing for large Froude numbers.
H. Zhang et al.
Nonlinear Bubble Competition of the Multimode Ablative Rayleigh-Taylor Instability and Applications to Inertial Confinement Fusion.
Physics of Plasmas, 27, 122701 (2020) [Cover Article] ▾ Digest ▾
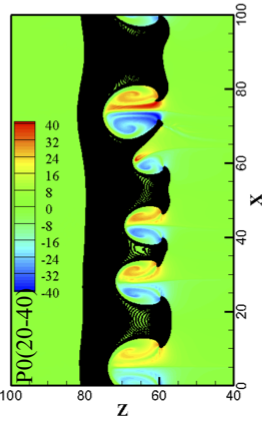
We carried out a thorough investigation of the multi-mode Rayleigh Taylor instability (RTI) under the influence of ablation, i.e. evaporation of mass due to a heat source such as in laser-driven plasmas. This work, which is a follow-up to Zhang et al., PRL (2018), provides further support that ablative RTI is qualitatively different in its evolution from classical RTI in the absence of ablation. This is because ablation leads to the generation of vorticity which leads to an enhanced growth of the instability, especially at the smallest scales, and prevents the RTI from transitioning into the so-called "bubble-merger" regime. We develop a model to describe the various stages of growth of the multi-mode ablative RTI and use it to explain the hydrodynamic stability boundary observed in fusion implosion experiments. Due to the dependence of ablative RTI on the initial perturbation amplitude and vorticity effect, ablative stabilization of the nonlinear ablative RTI in fusion experiments may not be as effective as expected if the initial perturbation is significant. We conclude that capsule surface roughness and laser imprint should be further reduced in order to improve the performance of so-called "low-adiabat" implosions.
F. Garcia-Rubio et al.
Self-Consistent Theory of the Darrieus-Landau and Rayleigh-Taylor Instabilities with Self-Generated Magnetic Fields.
Physics of Plasmas, 27, 112715 (2020) ▾ Digest ▾
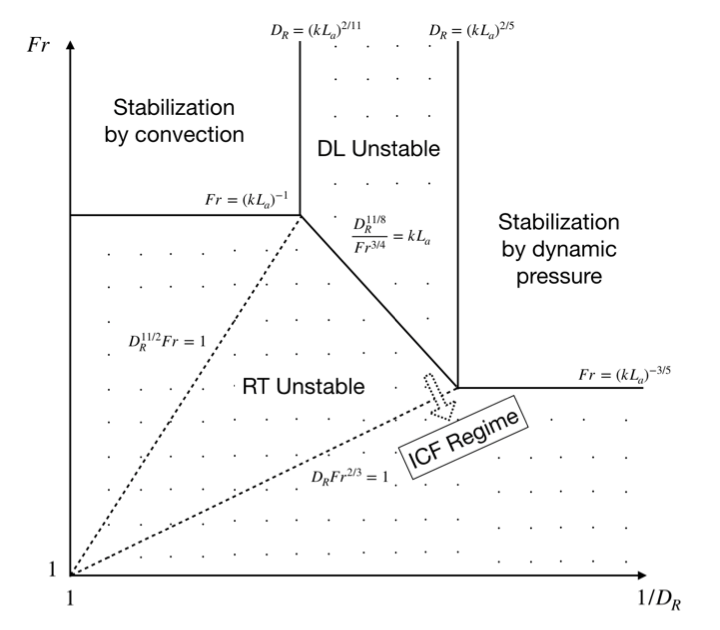
Short description goes here.
X. Bian et al.
Revisiting the Late-Time Growth of Single-mode Rayleigh-Taylor Instability and the Role of Vorticity.
Physica D: Nonlinear Phenomena, 403, 132250 (2020). [Invited paper] ▾ Digest ▾
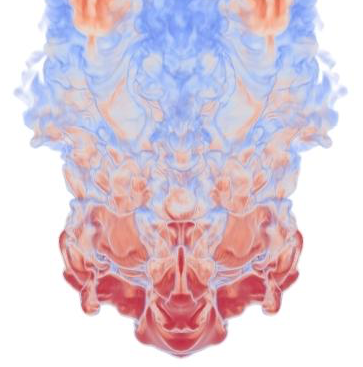
Short description goes here.
A. Lees and H. Aluie
Baropycnal Work: A Mechanism for Energy Transfer Across Scales.
Fluids, 4(2), 92 (2019). [Invited paper] ▾ Digest ▾
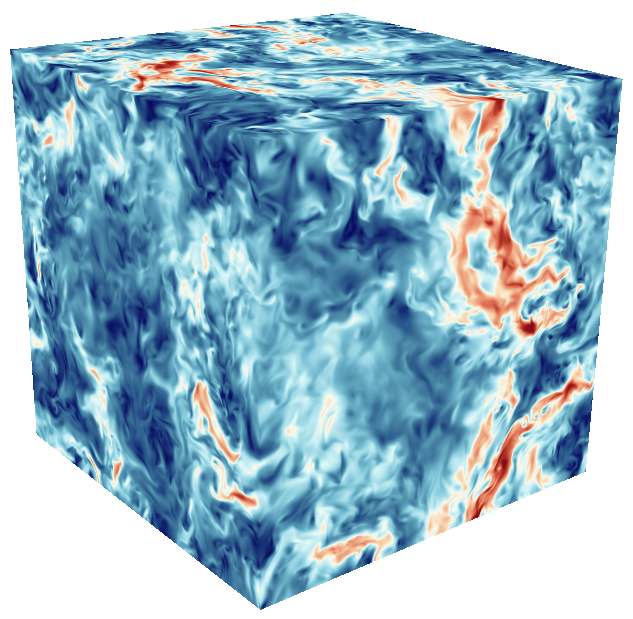
The role of baroclinicity, which arises from the misalignment of pressure and density gradients, is well-known in the vorticity equation, yet its role in the kinetic energy budget has never been obvious. Here, we show that baroclinicity appears naturally in the kinetic energy budget after carrying out the appropriate scale decomposition. Strain generation by pressure and density gradients, both barotropic and baroclinic, also results from our analysis. These two processes underlie the recently identified mechanism of "baropycnal work," which can transfer energy across scales in variable density flows. As such, baropycnal work is markedly distinct from pressure-dilatation into which the former is implicitly lumped in Large Eddy Simulations. We provide numerical evidence from 1,024^3 direct numerical simulations of compressible turbulence. The data shows excellent pointwise agreement between baropycnal work and the nonlinear model we derive, supporting our interpretation of how it operates.
X. Bian and H. Aluie
Decoupled cascades of kinetic and magnetic energy in magnetohydrodynamic turbulence.
Physical Review Letters, 122(13), 135101 (2019). ▾ Digest ▾
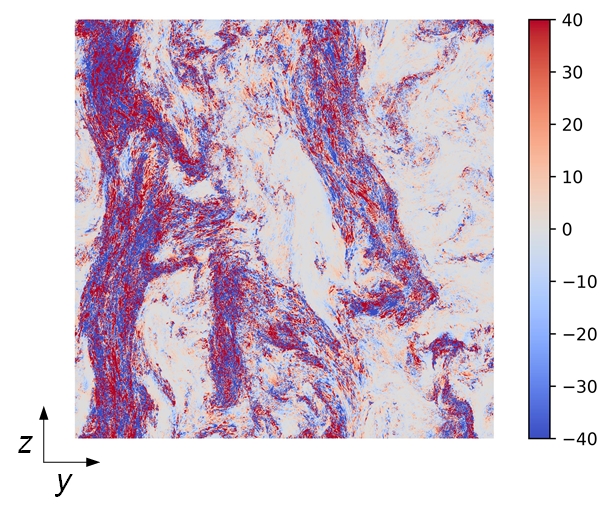
Flows which are coupled to magnetic fields (magnetohydrodynamic or MHD flows) are central to our understanding of a wide variety of systems ranging from the cosmological to the terrestrial. These include galaxies and clusters of galaxies, gas nebulae and the interstellar medium, star formation and evolution, solar wind and space weather, nuclear fusion, and metallurgy. In MHD flows, it is only total energy that is conserved and not magnetic and kinetic energy separately. As a manifestation of order emerging out of chaos (or permanence out of turbulence), we find that they are in fact conserved separately over a range of scales in turbulent flows. This essentially gives us two dynamical invariants (kinetic energy and magnetic energy) instead of just one (total energy). Invariants are highly prized quantities from which the governing laws of motion/evolution are derived. Our results have implications on the energetics and dissipation of these flows, the reconnection of magnetic field lines such as in solar flares, the amplification of magnetic field strength by dynamo action, and also on modeling efforts.
J. Xin et al.
Two mode coupling of the ablative Rayleigh Taylor instability.
Physics of Plasmas, 26, 032703 (2019) ▾ Digest ▾
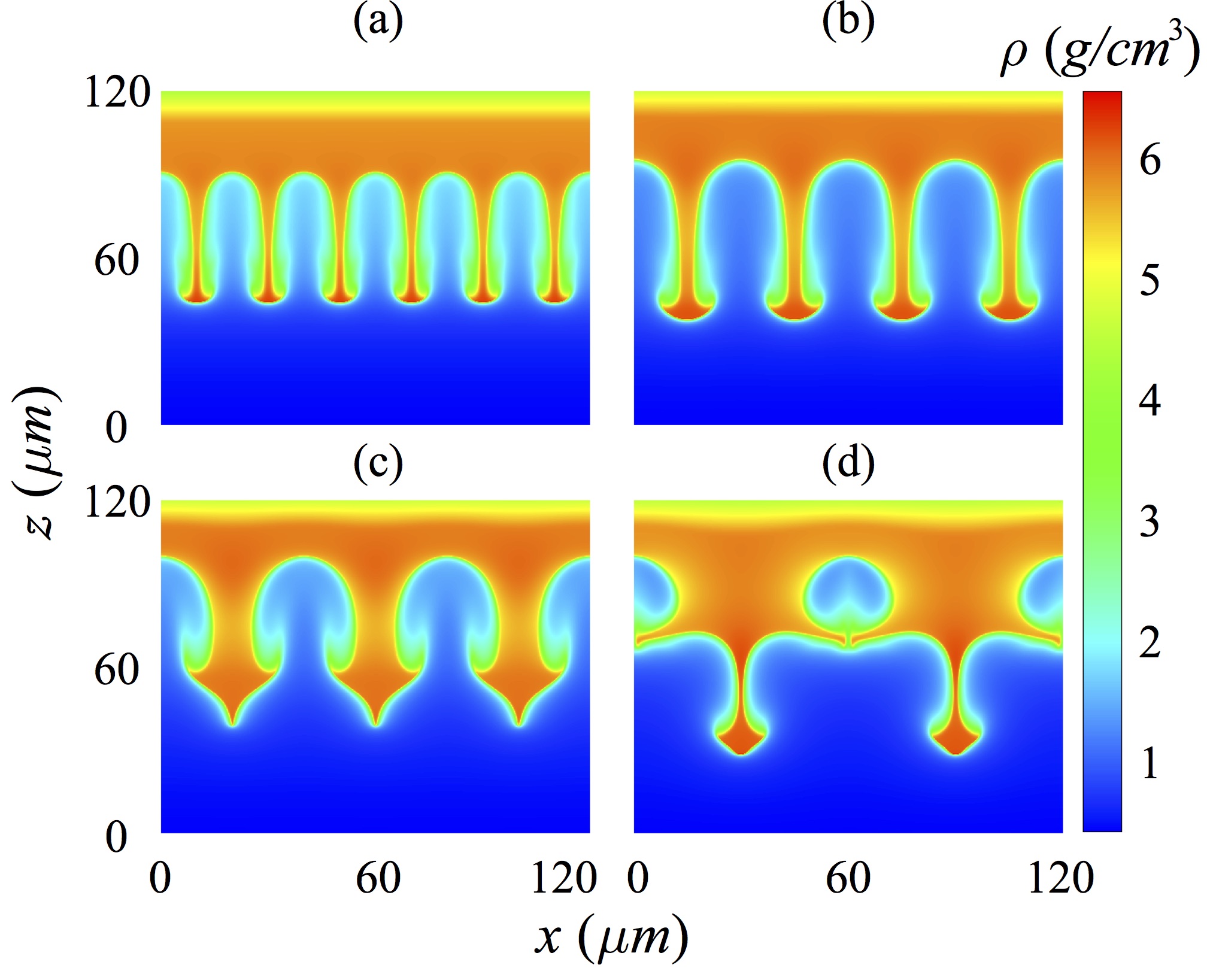
The paper explores the two mode coupling in ablative Rayleigh Taylor instability (RTI). These include coupling between short-short wavelengths and long-short wavelengths. We find that the presence of the short-wavelength mode in the long-short cases enhances the total ARTI bubble velocity. We also find that coupling of two short-wavelength modes forms a long-wavelength component which grows faster than each individual short-wavelength mode.
H. Aluie
Convolutions On The Sphere: Commutation With Differential Operators.
GEM: International Journal on Geomathematics, Springer, 10(9), 1-31 (2019) ▾ Digest ▾

This paper generalizes the definition of convolutions on spherical surfaces and proves that the new definition commutes with differential operators on the sphere. The motivation is to analyze (via coarse-graining) the multi-scale physics of flows in spherical geometries, such as atmospheric and oceanic flows, and in ICF. The paper provides the mathematical foundation for analyzing energy scale-transfer in the N. Atlantic Ocean. I had an unfortunate experience with the editorial process at another journal, Nonlinearity, the full account of which is here. I hope no one else has to go through such a nightmare scenario.
M. Sadek and H. Aluie
Extracting the Spectrum of a Flow by Spatial Filtering.
Physical Review Fluids, 3(12), 124610 (2018). ▾ Digest ▾
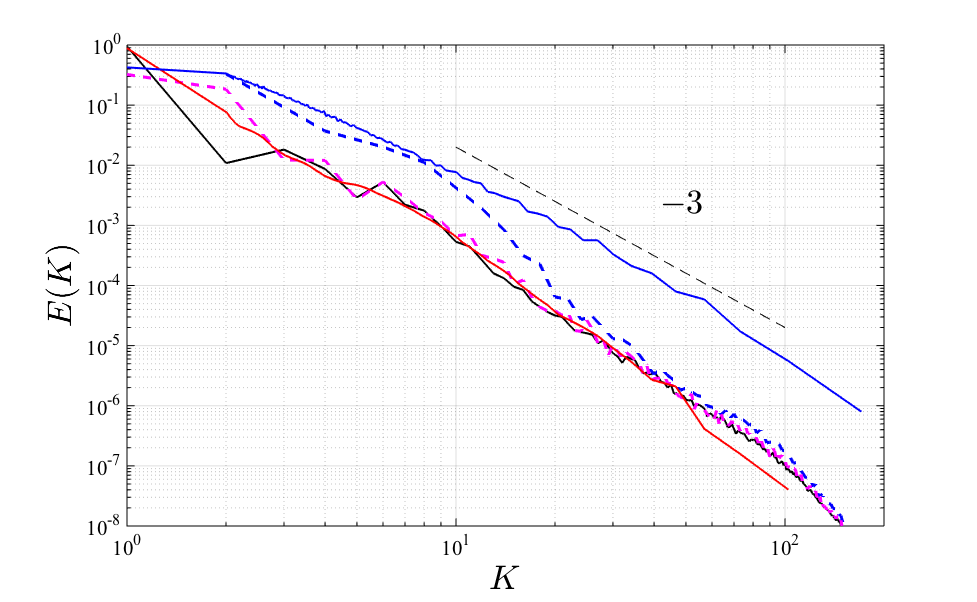
Can you gain “insight” by relinquishing some of your sight? Indeed, we show here how it is possible to quantify the energy content of various structures in a flow (i.e. measuring the spectrum) by observing the flow through “eyeglasses” of varying strength. In this paper, we show that the spectrum can be extracted within a local region by a straightforward filtering (averaging) in physical space which is equivalent to putting on weak eyeglasses. Our method guarantees energy conservation and can extract spectra of non-quadratic quantities self-consistently, such as kinetic energy in variable density flows, which the wavelet spectrum cannot. The method can be useful within coherent flow structures covering irregular regions, in multiphase flows, or in geophysical flows on Earth's curved surface.
H. Zhang et al.
Self-similar multimode bubble-front evolution of the ablative Rayleigh-Taylor instability in two and three dimensions.
Physical Review Letters, 121(18), 185002 (2018). ▾ Digest ▾
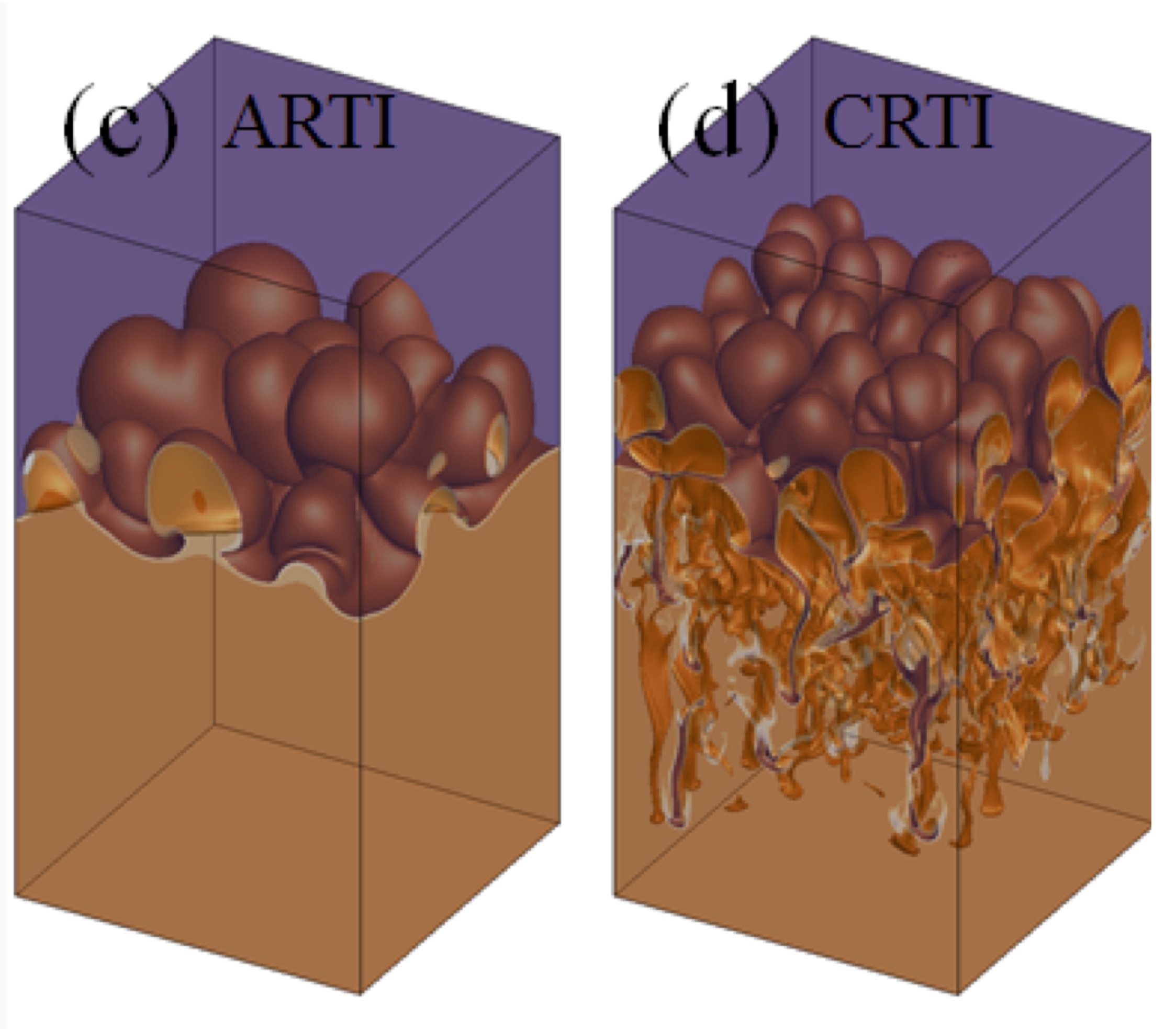
This paper completes the theoretical investigation of the ablative Rayleigh-Taylor Instability (aRTI) done in preceding works. Ablation (or mass evaporation) arises, for example, from radiative sources such in laser-driven plasmas or from UV stellar light in cold gaseous hydrogen clouds such as in the Eagle Nebula. Small-scale perturbations in the aRTI are often neglected because they are linearly stabilized by ablation. Here, we study the nonlinear evolution of these modes in the presence of an entire continuum of excitations, which we show lead to a self-similar growth of the instability. We find that while ablation reduces the growth of RTI if the initial perturbation is small, it enhances the growth if the perturbation is larger than a certain threshold. This is traced to enhanced vorticity generation due to ablation. Our work implies that the common practice of neglecting short wavelength modes in ICF and astrophysical modeling should be revisited.
K. M. Woo et al.
Impact of Three Dimensional Hot Spot Flow Asymmetry on Ion Temperature Measurements in Inertial Confinement Fusion Experiments.
Physics of Plasmas, 25, 102710 (2018) ▾ Digest ▾
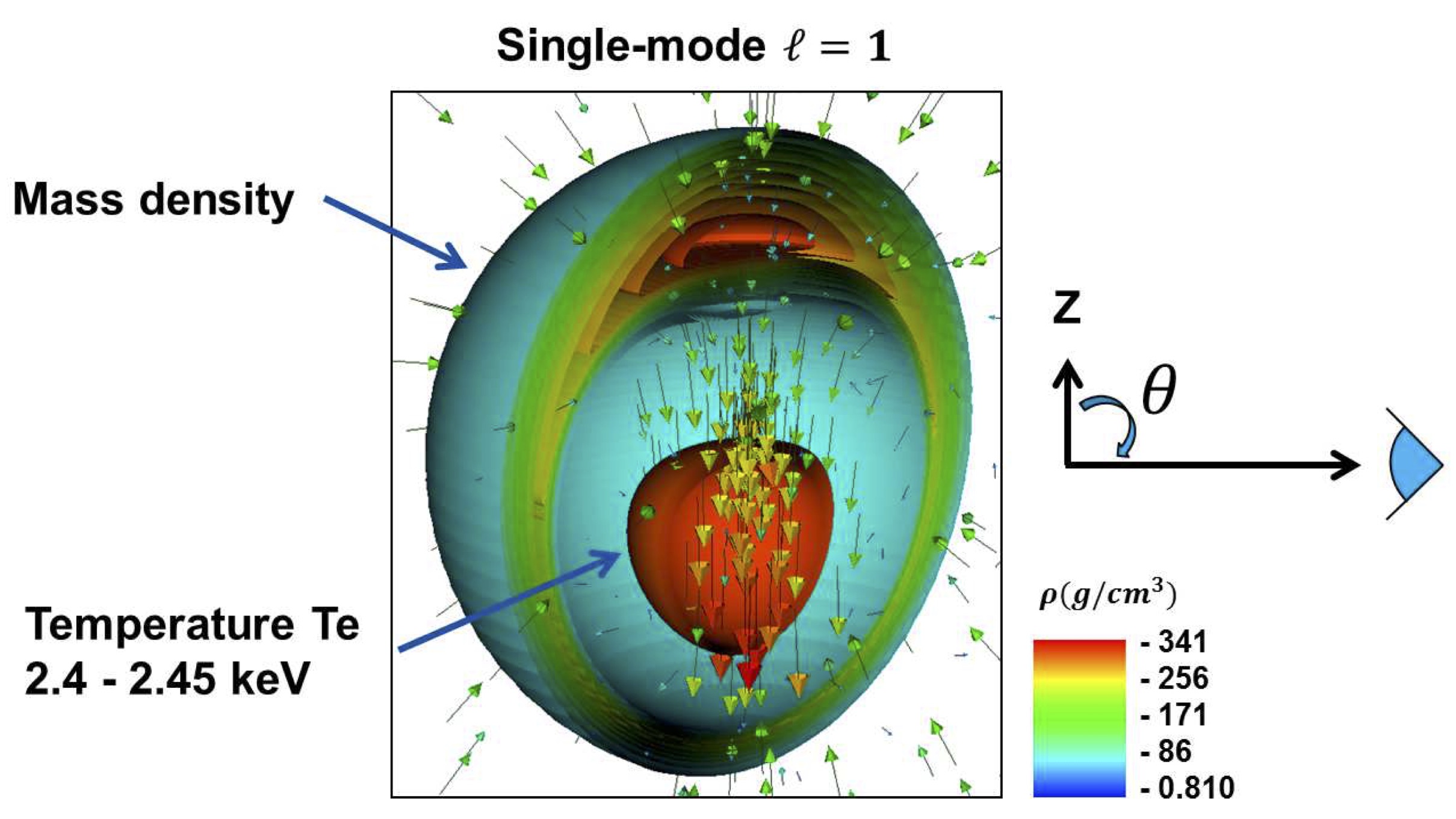
Deviations in inertial confinement fusion (ICF) implosions from 3D spherical symmetry lead to significant variations in inferred ion-temperature measurements in experiments. This work provides a consistent explanation for the 3D flow effects on inferred ion-temperature variations. It is shown that the effect of hot-spot flow asymmetry on variations in ion-temperature measurements is determined by six hot-spot flow parameters. Low wavenumber mode l=2 is shown to exhibit the largest total velocity variance and leads to inferred ion temperature well above the thermal ion temperature. The paper also provides a formula which allows for improving the predictions of thermal ion temperatures.
K. M. Woo et al.
Effects of residual kinetic energy on yield degradation and ion temperature asymmetries in inertial confinement fusion implosions.
Physics of Plasmas, 25(5), 054603 (2018) ▾ Digest ▾
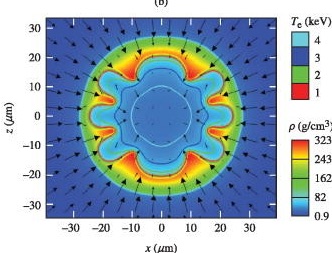
This paper studies the Rayleigh–Taylor instability in inertial confinement fusion implosions. It is shown that larger hot-spot volumes observed in low modes and the consequential pressure degradation can be explained in terms of increasing the residual kinetic energy. The low mode asymmetries are shown to cause the largest ion temperature variations in the mode spectrum.
D. Zhao, H. Aluie
The Inviscid Criterion for Decomposing Scales.
Physical Review Fluids, 3, 054603 (2018) ▾ Digest ▾
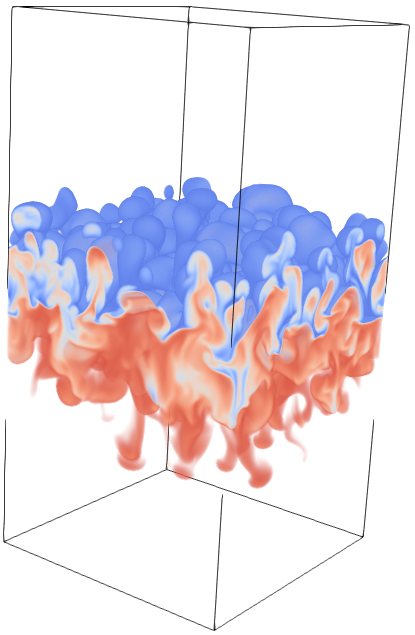
This paper pertains to the fundamental notion of "length-scale" and how to disentangle scale interactions in flows with significant density variations, such as high-speed, reactive, or multi-phase flows. A “length scale” in a fluid flow does not exist as an independent entity but is associated with the specific flow variable being analyzed. While this might seem obvious, we often discuss the “inertial range” or the “viscous range” of length scales in turbulence as if they exist independently of a flow variable, which in incompressible turbulence is the velocity field. How should we analyze “length-scales” in flows with significant density variations?
M. Buzzicotti, H. Aluie, L. Biferale, M. Linkmann
Energy transfer in turbulence under rotation.
Physical Review Fluids, 3, 034802 (2018) ▾ Digest ▾
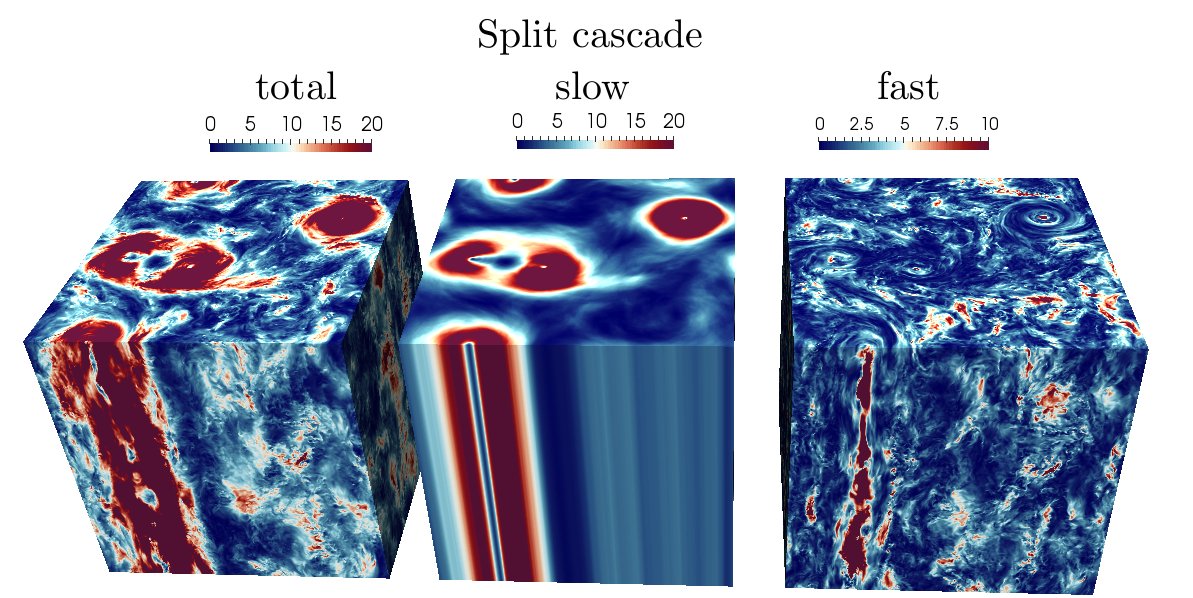
Two different mechanisms are known to be able to transfer energy upscale in a turbulent flow. The first is characterized by two-dimensional interactions among triads lying on the two-dimensional, three-component (2D3C)/slow manifold. The second mechanism is three-dimensional and consists of interactions between triads with the same sign of helicity (homochiral). Here, we find that the upscale cascade at wave numbers close to the forcing scale is generated by increasingly dominant homochiral interactions which couple the three-dimensional bulk to the 2D3C plane. This coupling produces an accumulation of energy in the 2D3C plane, which then transfers energy to smaller wave numbers thanks to the two-dimensional mechanism.
H. Zhang, R. Betti, V. Gopalaswamy, R. Yan, H. Aluie
Nonlinear excitation of the ablative Rayleigh-Taylor instability for all wave numbers.
Physical Review E, 97, 011203(R) (2018) ▾ Digest ▾
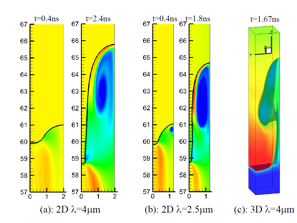
Ablation (or mass evaporation) arises, for example, from radiative sources such as lasers in laser-driven plasmas or from UV stellar light in cold gaseous hydrogen clouds such as in the Eagle Nebula. Small-scale perturbations in the ablative Rayleigh-Taylor instability (ARTI) are often neglected because they are linearly stabilized by ablation. Here, we show that modes of any wavelength can be destabilized if they are nonlinear (large amplitude perturbation). We find that for conditions found in laser fusion targets, the often neglected short wavelength ARTI modes are more efficient at driving mixing of ablated material throughout the target.
M. Buzzicotti, M. Linkmann, H. Aluie, L. Biferale, J. Brasseur, C. Meneveau
Effect of filter type on the statistics of energy transfer between resolved and subfilter scales from a-priori analysis of direct numerical simulations of isotropic turbulence.
Journal of Turbulence, 19(2), 167-197 (2018) ▾ Digest ▾
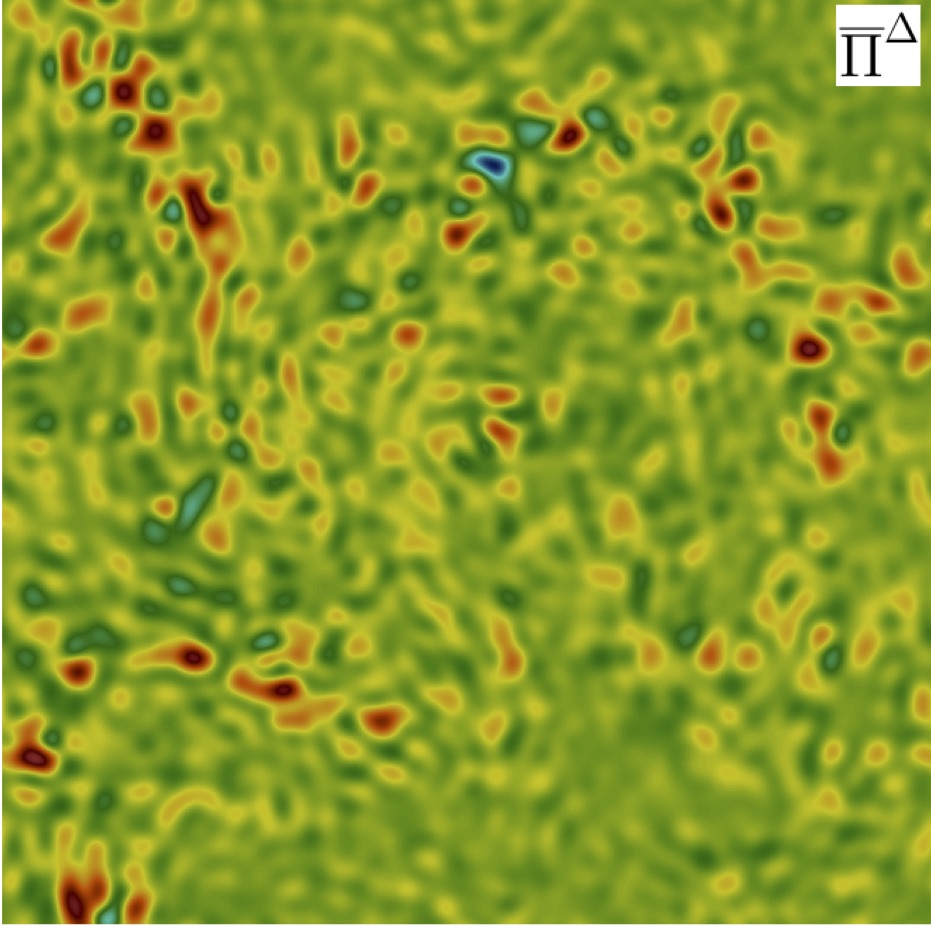
Energy scale-transfer sensitivity to filtering kernel, including a novel class of Galerkin projectors.
H. Aluie, M. Hecht, G. Vallis
Mapping the Energy Cascade in the North Atlantic Ocean: The Coarse-graining Approach.
Journal of Physical Oceanography, 48 (2), 225-244 (2018) ▾ Digest ▾
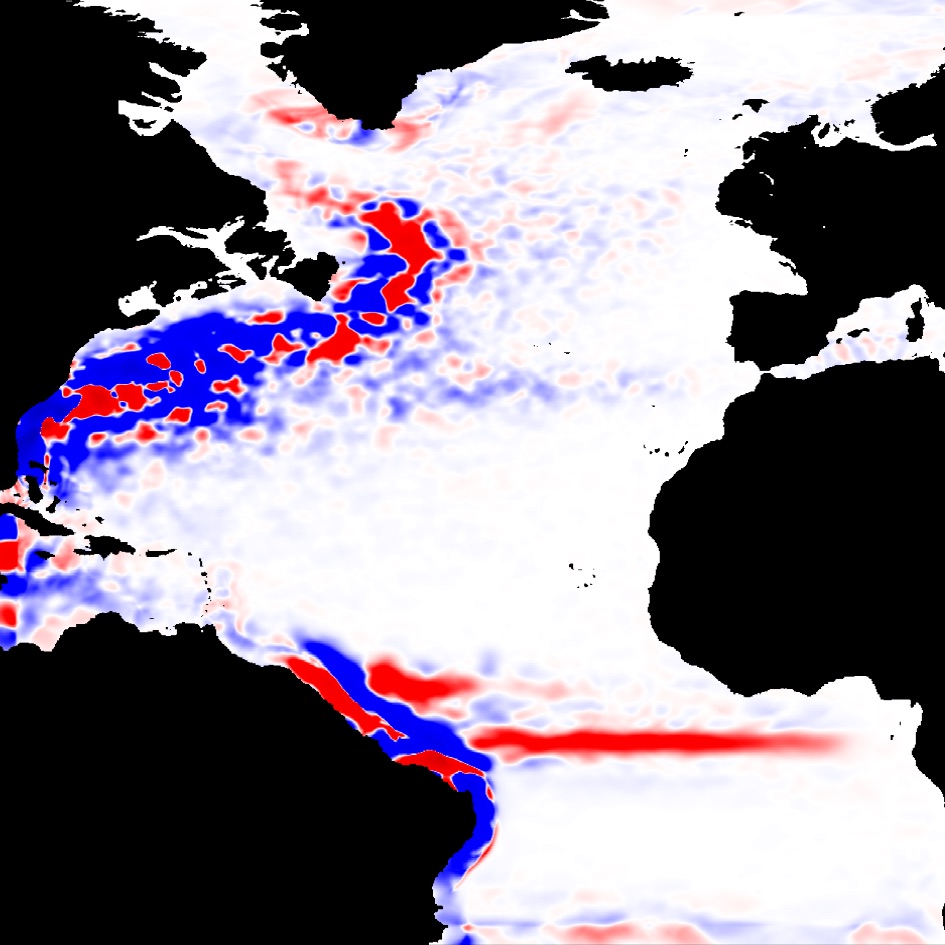
This paper is a culmination of interdisciplinary work spanning applied mathematics, physical oceanography, and turbulence. What started off as a seemingly straightforward application of methods from turbulence to oceanic data turned out to require new theoretical developments in applied mathematics, considerable effort in numerical implementation, and a few years to finish. I believe this was a worthy investment to provide tools that will hopefully prove valuable in atmospheric and oceanic dynamics, in climate science, and also in general flows with spherical geometry such as imploding targets in inertial confinement fusion power. The mathematical developments underpinning this analysis are published here.
H. Aluie
Coarse-Grained Incompressible Magnetohydrodynamics: analyzing the turbulent cascades. (Invited paper)
New Journal of Physics, 19, 025008 (2017) ▾ Digest ▾
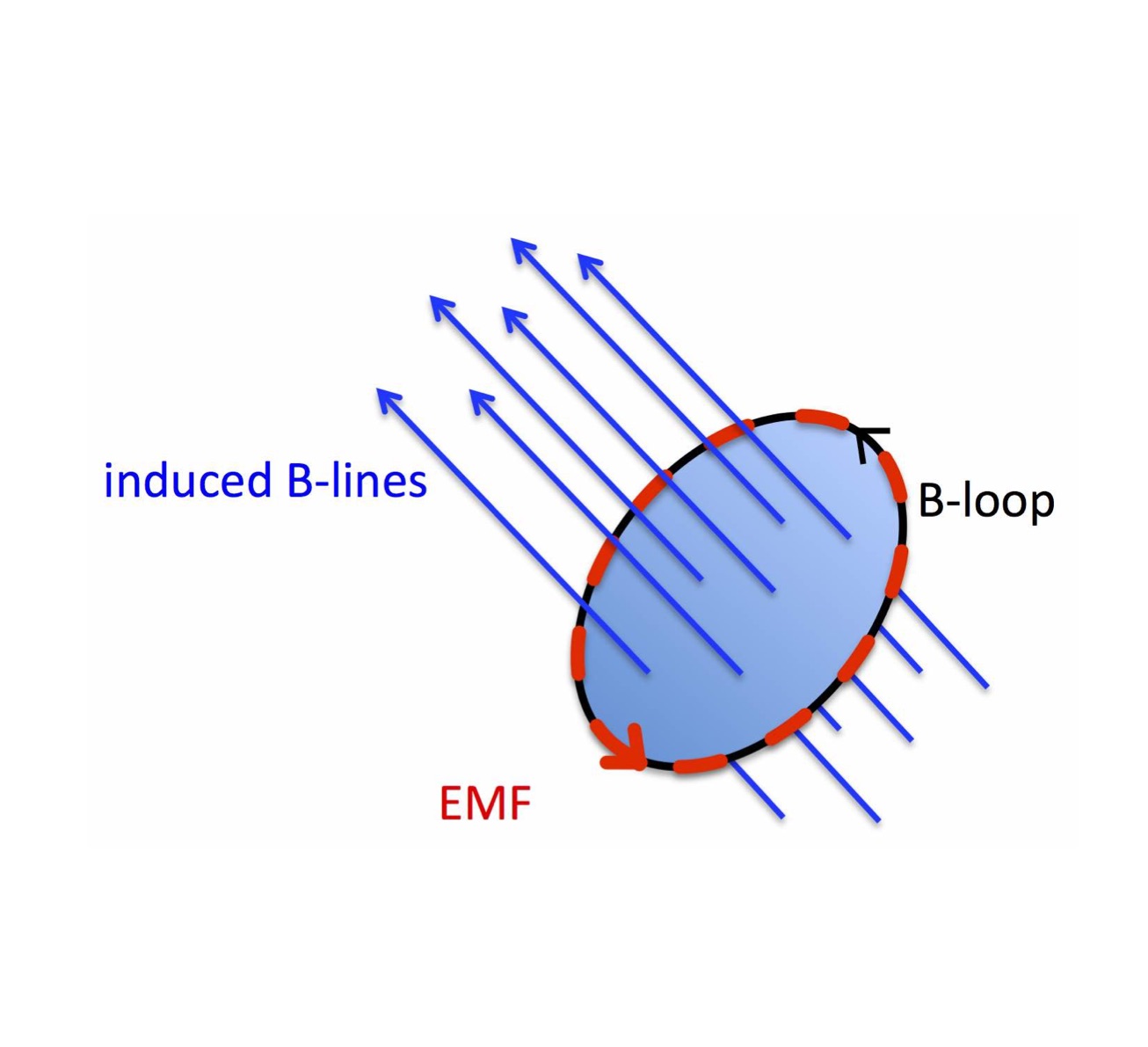
This work, which was mostly done in collaboration with G. Eyink, formulates the coarse-graining (or filtering) approach in MHD flows from a first-principles physics stand-point. The approach is a powerful framework to study the multi-scale physics of flows, including MHD turbulence. A key result is the proof that magnetic helicity, unlike energy, cannot undergo a cascade to arbitrarily small scales. Magnetic helicity is an important topological quantity in MHD flows that quantifies the degree of knottedness of magnetic field lines. The paper also reviews the concept of a cascade, but within the coarse-graining framework, and attempts to explain intuitively how “rough” flows can dissipate energy without the aid of viscous (or microphysical) processes.
R. Yan, R. Betti, J. Sanz, H. Aluie, B. Liu, A. Frank
Three-dimensional single-mode nonlinear ablative Rayleigh-Taylor instability.
Physics of Plasmas, 23 (2), 022701 (2016) ▾ Digest ▾

This paper studies the single mode Rayleigh-Taylor instability (RTI) in the presence of ablation (or mass evaporation). Ablation arises, for example, from radiative sources such as lasers in laser-driven plasmas or from UV stellar light in cold gaseous hydrogen clouds such as in the Eagle Nebula. While ablation has been known to slow down and even suppress the RTI in the linear (small amplitude) regime, here we show that ablation can exacerbate the instability in the nonlinear regime due to vorticity generation.
M. K. Rivera, H. Aluie, R. E. Ecke
The direct enstrophy cascade of two-dimensional soap film flows.
Phys. Fluids, 26, 055105 (2014) ▾ Digest ▾
Short description goes here.
G. L. Eyink, E. T. Vishniac, C. Lalescu, H. Aluie, K. Kanov, K. Burger, R. Burns, C. Meneveau, A. Szalay
Flux-freezing breakdown observed in high-conductivity magnetohydrodynamic turbulence.
Nature, 497, 466-469 (2013) ▾ Digest ▾
Short description goes here.
H. Aluie
The range of scale coupling and the cascade in the presence of shocks.
arXiv:1101.0150 (submitted) ▾ Digest ▾
Short description goes here.
H. Aluie
Scale decomposition in compressible turbulence.
Physica D: Nonlinear Phenomena, 247(1), 54-65 (2013) ▾ Digest ▾
Short description goes here.
H. Aluie, S. Li, H. Li
Conservative cascade of kinetic energy in compressible turbulence.
Astrophysical Journal Letters, 751, L29 (2012) ▾ Digest ▾
Short description goes here.
H. Aluie, S. Kurien
Joint downscale fluxes of energy and potential enstrophy in rotating stratified Boussinesq flows.
Europhysics Letters, 96, 44006 (2011) ▾ Digest ▾
Short description goes here.
H. Aluie
Compressible turbulence: The cascade and its locality.
Physical Review Letters, 106, 174502 (2011) ▾ Digest ▾
Short description goes here.
H. Aluie, G. L. Eyink
Scale locality of magnetohydrodynamic turbulence.
Physical Review Letters, 104, 081101 (2010) ▾ Digest ▾
Short description goes here.
G. L. Eyink, H. Aluie
Localness of energy cascade in hydrodynamic turbulence. I. Smooth coarse graining.
Physics of Fluids, 21, 115107 (2009) ▾ Digest ▾
Short description goes here.
H. Aluie, G. L. Eyink
Localness of energy cascade in hydrodynamic turbulence. II. Sharp spectral filter.
Physics of Fluids, 21, 115108 (2009) ▾ Digest ▾
Short description goes here.
G. L. Eyink, H. Aluie
The breakdown of Alfven's theorem in ideal plasma flows: Necessary conditions and physical conjectures.
Physica D: Nonlinear Phenomena, 223, 82 (2006) ▾ Digest ▾
Short description goes here.
